So, in practical mobile robot motion planning, we want to have a nice trajectory, which does not only avoids collision with other agents, but is also kinematically feasible.

To achieve this, we can use optimization based algorithms. Given a feasible initial trajectory, and properly bootstraped costs, we are able to get the optimal trajectory with iterative linear quadratic regulation.

We're basically able to define cost of any shape, on any kinematic terms, including position, velocity and even acceleration. In iterative LQR, we find the local quadratic approximation of the cost functions, and run LQR to get the input of the next iteration. We can end the iteration based on some criterial, like absolute tolerance or relative tolerance -- if the optimization step can not change the trajectory much, we should be very close to the minima. Or the local minima :/

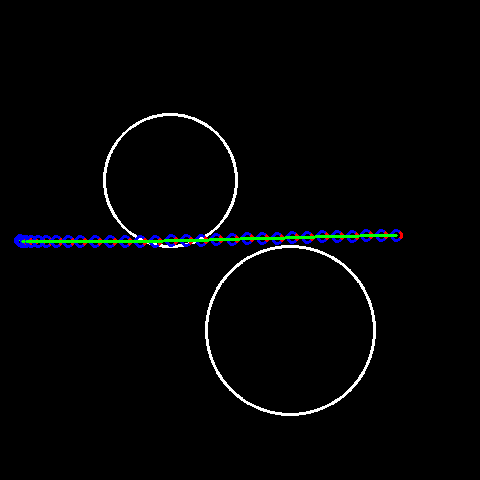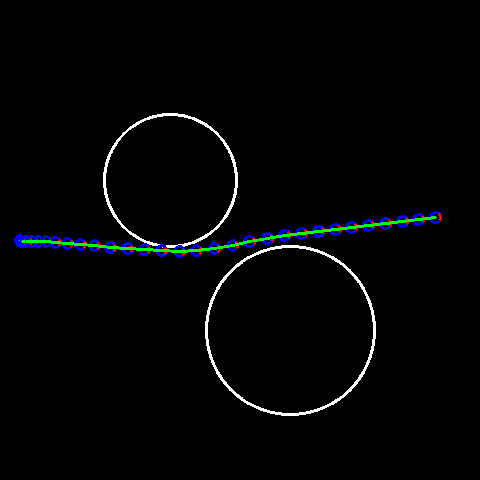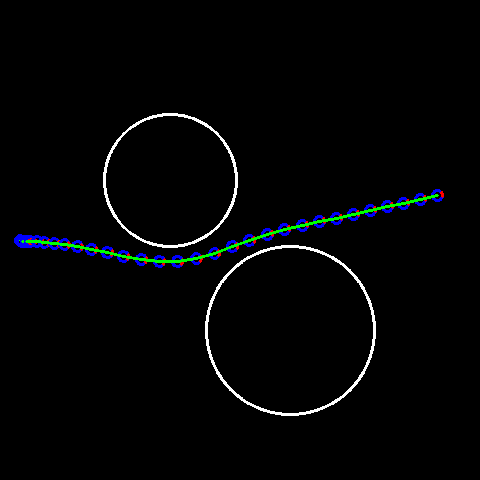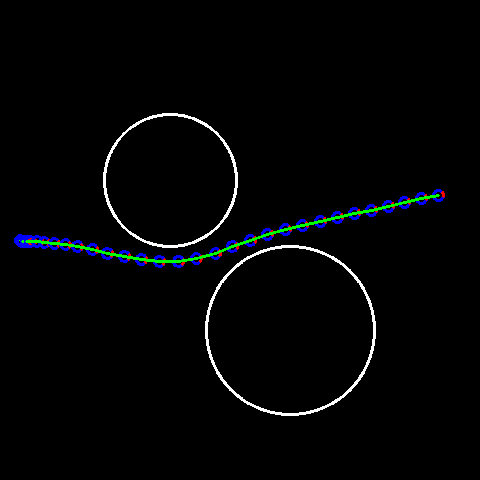
As shown in the gif to the left, with the zero control initialization, we found a trajectory which stayed away from the objects. Things could be trickier if we have different type of costs, or if we have worse initialization (which may drive the car off the road in the worst cases).